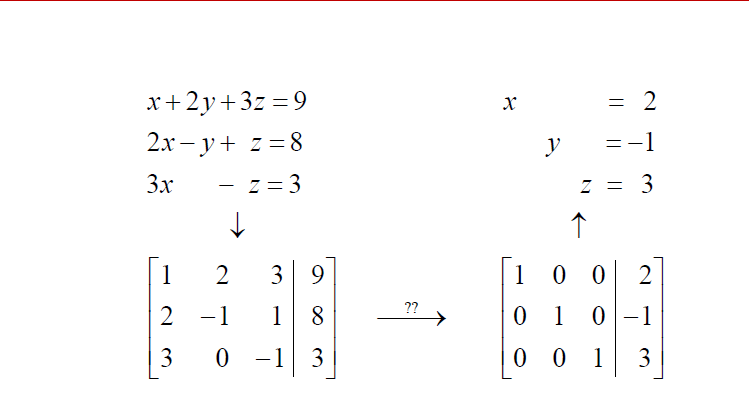A matrix in that form is said to be in the reduced row echelon form.

What is reduced row echelon form. Typically, these are given as (1). The echelon form of a matrix isn't unique, which means there are infinite answers possible when you perform row reduction. The first number in the row (called a leading coefficient) is.

Row operations are performed until the. Anyway, it is worth to note that for an invertible matrix, the. What is the purpose of a reduced row echelon form?

This means that the matrix meets the following three requirements: From a theoretical point of view, the reduced form has the advantage of being uniquely defined for a given matrix. What is row echelon form?

Reduced row echelon form [ edit] a matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions: Chauke chain rule case ii heartland senior prof e. A matrix is in reduced row echelon form (rref) if the three conditions in de nition 1 hold and in addition, we have 4.

Your summaries of 'row echelon' and 'reduced row echelon' are completely correct, but there is a slight issue with the rules for elimination. All zero rows (if any) belong at the bottom of the matrix. For reduced row echelon form, the leading 1 of every row contains 0 below and above its in that column.

Identify the last row having a pivot equal to 1, and let this be the pivot row. Reduced row echelon form educational content senior prof e. Row echelon form is any matrix with the following properties: