A full circle is 360°, so that leaves 360° − 2×40° = 280°.

Vertical angles theorem. Therefore, ∠ b is also 47 0 (vertical angles are congruent or equal). The vertical angles theorem states that the opposite (vertical) angles of two intersecting lines are. If two angles are vertical angles, then they have equal measures.

∠a and ∠d are adjacent angles and ∠c and ∠b are. Angles a° and c° are also vertical. Then, by linear pair postulate, they are supplementary.

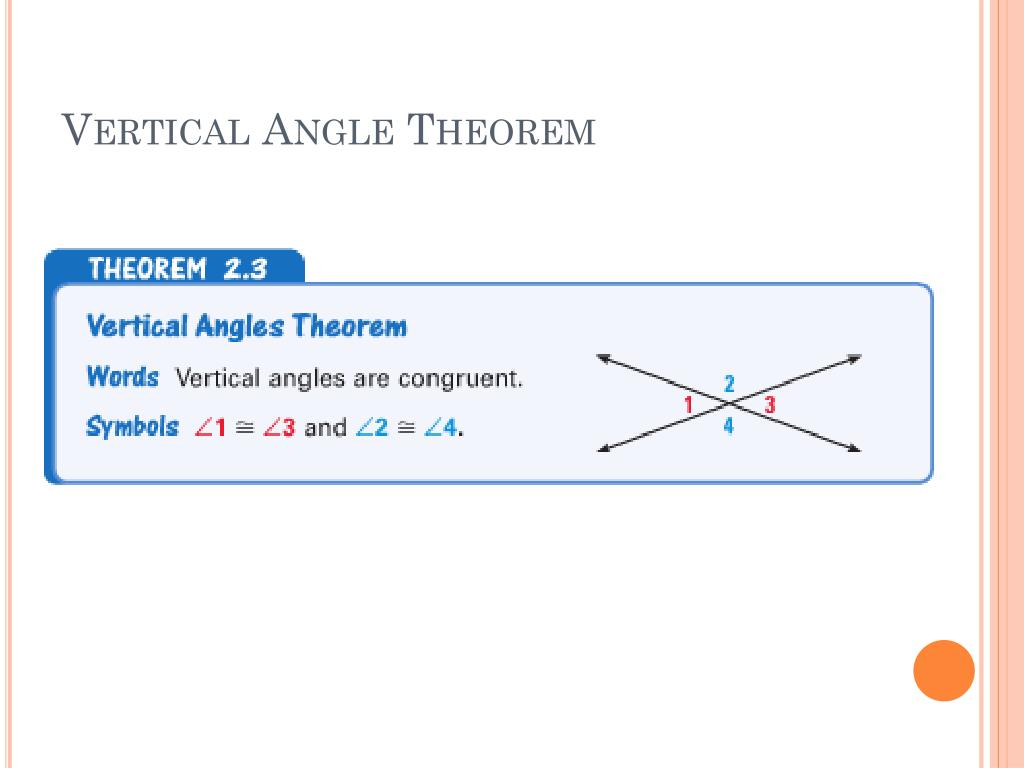
In picture 2, ∠ 1 and ∠ 2 are vertical angles. Vertical angles are the angles formed by the intersection of two lines. Vertical angles theorem states that vertical angles, angles that are opposite each other and formed by two intersecting straight lines, are congruent.

Calculate the unknown angles in the following figure. Vertical angle examples example 1. For example, in the diagram below, we have two pairs of vertical angles.

In the diagram above, since angles 1 and 2 are adjacent and form a straight. Angles a and b and angles c and d are pairs of. The vertical angle theorem states that two opposite vertical angles formed by two lines intersecting each other are always equal (congruent).

M ∠ x in digram 1 is 157 ∘ since its vertical angle is 157 ∘. ∠ 47 0 and ∠ b are vertical angles. Like the rest of these, the vertical angles theorem serves a foundational role in the rules of geometry and trigonometry.