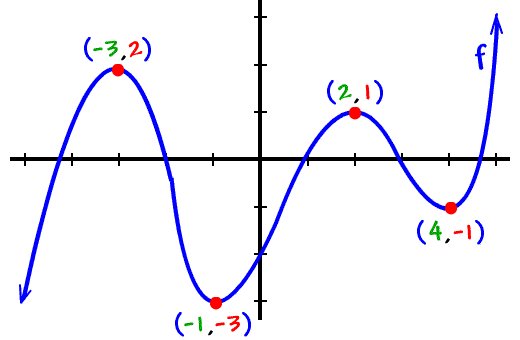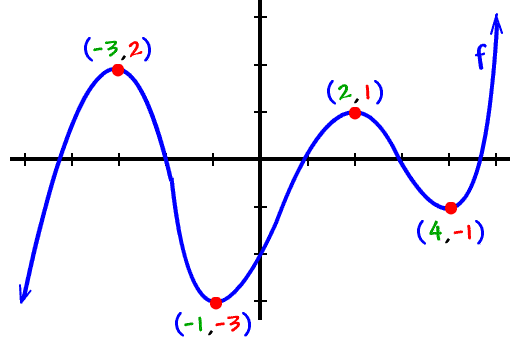
Here the relative extrema are in red with x 2 a local max and x 3 a local min.

Relative extrema on a graph. The max is, actually, the height. Finding all critical points and all points where is. The value of x within the domain of f (x), which is neither a local maximum nor a local minimum, is called the point of.

The x guy is where the max occurs. Relative extrema on graph a function can have more than one relative extrema but there can only be one absolute maximum and absolute minimum point. Compare the graphs of f ( x) = x 3 + 1 and f ′ ( x) = 3 x 2.

Relative extrema is a fancy term for the maximum and minimum points of a graph, relative to nearby points. So we start with differentiating : Local extrema (relative extrema) local extrema are the smallest or largest outputs of a small part of the function.

Notice that f ′ ( x) does not change. And this one over here is a relative minimum point. F has a relative max of 1 at x = 2.

The word “extrema” is plural for the word “extremum”. To do this, find your first derivative and then find where it is equal to. For example, the function y = x 2 goes to infinity, but you can.

We still do not have the tools. To find the exact values (coordinates) for these points, use the three. Now let's do an example dealing with absolute extrema.