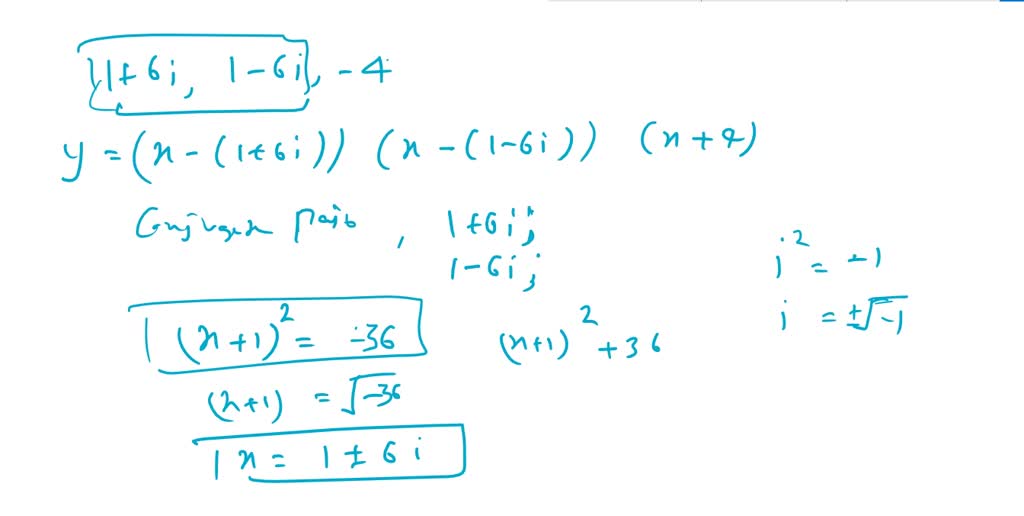
The question implies that all of the zeros of the cubic (degree 3) polynomial are at the same point, x = 9.

How to find the zeros of a polynomial function degree 3. We know, that the cubic function can have one, two or three roots. You can use the intermediate value theorem. If the function has a root, then prove it.

If you have a complex root, then you know you also have a root that is its conjugate: Find a polynomial function with real coefficients that has the given zeros. Now that we can find rational zeros for a polynomial function, we will look at a theorem that discusses the number of complex zeros of a polynomial function.

Evaluate a polynomial using the remainder theorem. If not, then explain why. In the last section, we learned how to divide polynomials.

You can put this solution on your website!. For a quadratic equation of the form ax 2 + bx + c = 0 with the coefficient a, b, constant term c, the sum and. This video provides an example of how to find the zeros of a degree 3 polynomial function with the help of a graph of the function.

The zeros of the quadratic equation are represented by the symbols α, and β. Use the linear factorization theorem. Factoring polynomials helps us determine the zeros or solutions of a function.

For these cases, we first equate the polynomial function with zero and form an equation. Now that we can find rational zeros for a polynomial function, we will look at a theorem that discusses the number of complex zeros of a polynomial function. This is guess and check until you hone in on the roots.