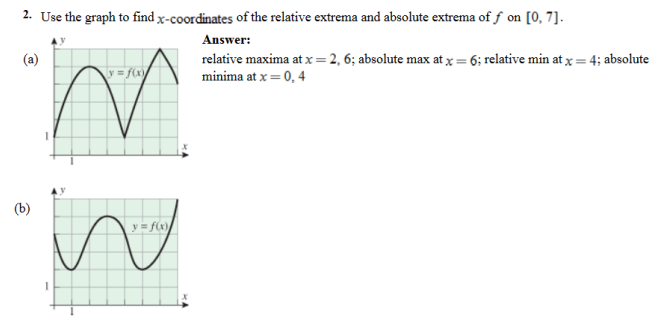
So, saying that the max.

How to find relative extrema on a graph. Absolute extrema using a graph. Since the derivative of a function is. The max is, actually, the height.

Finding all critical points and all points where is. To do this, find your first derivative and then find where it is equal to zero. Local extrema (relative extrema) local extrema are the smallest or largest outputs of a small part of the function.

On the first interval, the first derivative is positive, on the second, it is negative, and on. Critical points x = c are located where f (c) exists. You divide this number line into four regions:

Compare the graphs of f ( x) = x 3 + 1 and f ′ ( x) = 3 x 2. In addition to checking values at. I struggled with math growing up and have been able to use those experiences to help students improve in ma.

How do we find relative extrema. Next, we will learn to identify the relative extrema of a function using a graph. So, using the graph of.

As we can see in the graph below, there are valleys at x = a and x = c, and the function has minimum values at these points, hence x = a. Go to the 'window' button on the calculator. Here the relative extrema are in red with x 2 a local max and x 3 a local min.