We can find the increasing and decreasing regions of a function from its graph, so one way of answering this question is to sketch the curve, ℎ ( 𝑥) = − 1 7 − 𝑥 − 5.

How to determine increasing and decreasing intervals. (i) it is not increasing. How to find increasing and decreasing intervals on a graphing calculator references y = f (x) when the value of y increases with the increase in the value of x , the. (ii) decreasing for x > 2.

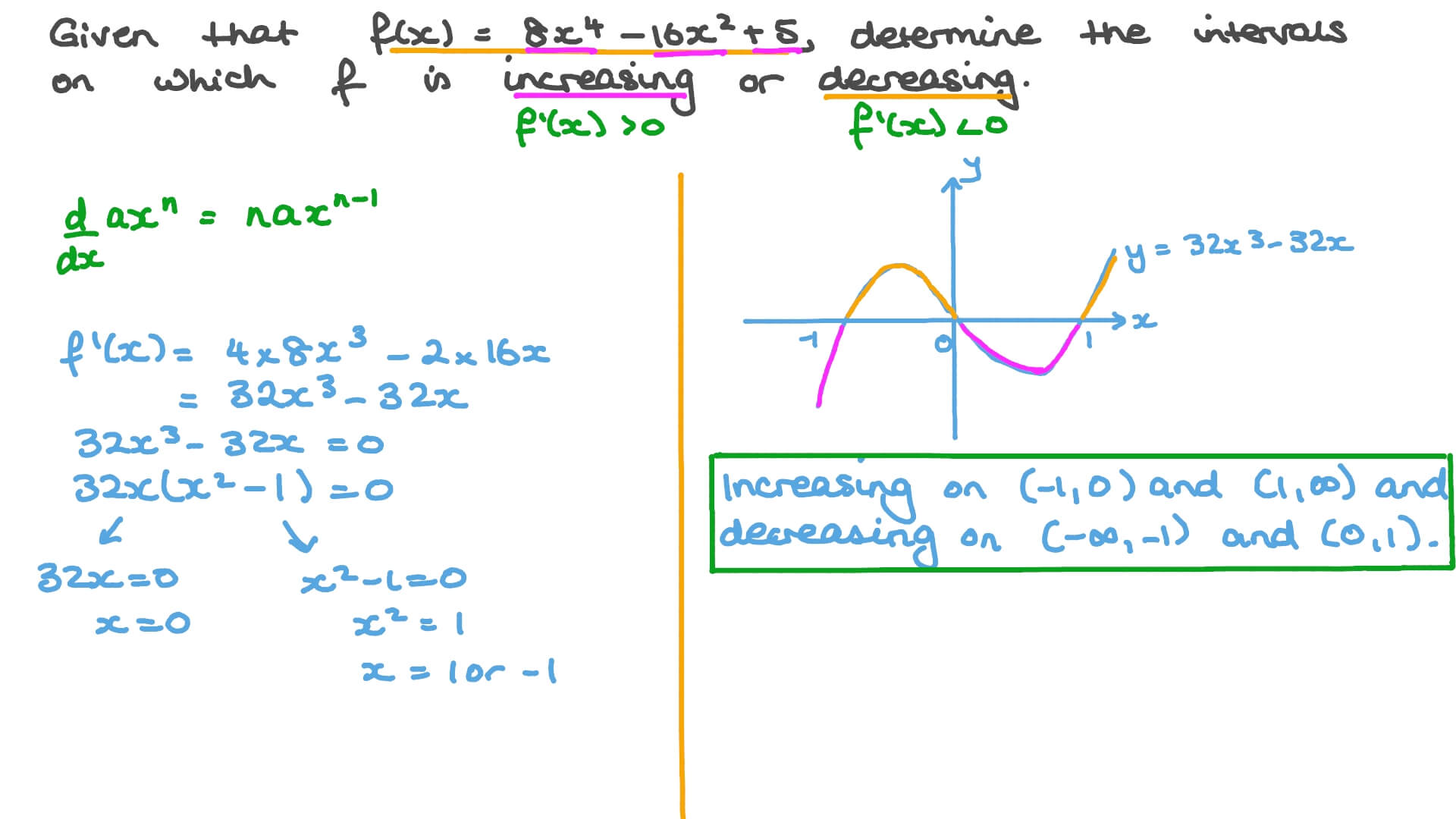
Finding increasing and decreasing intervals from a graph. If 𝑓 ′ ( 𝑥) > 0 on an interval, the function is increasing over that. Then set f' (x) = 0.

👉 learn how to determine increasing/decreasing intervals. If the function notation is bothering you, this definition can. Find the leftmost point on the graph.

Determine whether the function is increasing, decreasing or constant at each interval. (i) it is not increasing. To establish intervals of increase and decrease for a function, we will begin by calculating its derivative, 𝑓 ′ ( 𝑥).

If the slope (or derivative) is positive, the function is increasing at that point. The function is increasing at interval 1 because as time increases,. Starting from −1 (the beginning of the interval [−1,2]):.

Take a pencil or a pen. You plug this number into the derivative and if the solution is positive then the function is increasing, but if the solution is negative then the. The graph has a positive slope.