Garfield um das jahr 1875 ein beweis entwickelt und bei der zeitschrift new england journal of education eingereicht und sogar veröffentlicht.

Beweis satz des pythagoras. 4.13 der wahrscheinlich eleganteste beweis des theorems von pascal v. Er fand heraus, dass die zwei quadrate, die an den kurzen seiten (katheten) eines rechtwinkligen dreiecks gebildet werden können, zusammengenommen genau den gleichen flächeninhalt haben, wie das quadrat, das an der längsten seite (hypotenuse) eines solchen dreiecks zu bilden ist. Satz des pythagoraskathetensatzh ohensatz anwendungen es gilt satz des pythagoras ,kathetensatz ,h ohensatz.

Der satz des pythagoras lautet a²+b²=c², was soviel bedeutet, die quadrate über den katheten im rechtwinkligen dreieck sind gleich dem hypotenusenquadrat. Beweis des kathetensatzes (aus 'pythagoras' und höhensatz) a 2 = p 2 + h 2 = p 2 + p · q = p(p + q) = p · c analog für b 2 = q · c Allerdings ist der satz des pythagoras, die geschichte der schöpfung und die beweise für seine schranke für die meisten ist es mit diesen wissenschaftlern.

(p + q) 2 = p 2 + 2h 2 + q 2, also p 2 + 2pq + q 2 = p 2 + 2h 2 + q 2, also p · q = h 2. 13.3.2018 gliederung 1.der satz des pythagoras 1.1 der satz des pythagoras einfach erklärt 1.2 anwendung des satzes des pythagoras 2.mathematik und philosophie 3.der einfluss der mathematik auf die harmonielehre 4. Nachstehend ein beweis ausführlich festgehalten.

Für den beweis des satzes gibt es zahlreiche verschiedene möglichkeiten. In diesem clip wird die grafische lösung des satzes des phytagoras gezeigt. Der satz des pythagoras gilt für alle rechtwinkligen dreiecke und lautet:

In einem solchen beweis wird eine gleichung aufgestellt, aus der die gleichung a 2 + b 2 = c 2 folgt. A2 + b2 = c2. Die ergänzungsgleichheit ist ein wichtiges prinzip der mathematik.

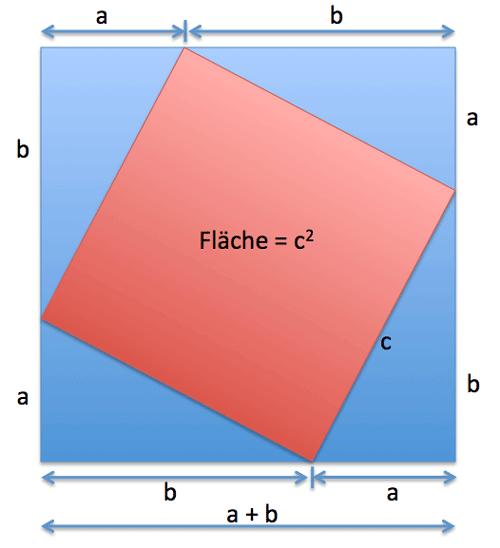
A 2 + b 2 = c 2 a^2+b^2=c^2 a 2 + b 2 = c 2. Andererseits besteht es aus einem kleinen quadrat der fläche c2 c 2 und vier. Neben den geometrischen beweisen gibt es auch algebraische beweise für den satz des pythagoras.