Hello, in this particular article you will provide several interesting pictures of wert einer reihe berechnen.html. We found many exciting and extraordinary wert einer reihe berechnen.html pictures that can be tips, input and information intended for you. In addition to be able to the wert einer reihe berechnen.html main picture, we also collect some other related images. Find typically the latest and best wert einer reihe berechnen.html images here that many of us get selected from plenty of other images.
 We all hope you can get actually looking for concerning wert einer reihe berechnen.html here. There is usually a large selection involving interesting image ideas that will can provide information in order to you. You can get the pictures here regarding free and save these people to be used because reference material or employed as collection images with regard to personal use. Our imaginative team provides large dimensions images with high image resolution or HD.
We all hope you can get actually looking for concerning wert einer reihe berechnen.html here. There is usually a large selection involving interesting image ideas that will can provide information in order to you. You can get the pictures here regarding free and save these people to be used because reference material or employed as collection images with regard to personal use. Our imaginative team provides large dimensions images with high image resolution or HD.
 wert einer reihe berechnen.html - To discover the image more plainly in this article, you are able to click on the preferred image to look at the photo in its original sizing or in full. A person can also see the wert einer reihe berechnen.html image gallery that we all get prepared to locate the image you are interested in.
wert einer reihe berechnen.html - To discover the image more plainly in this article, you are able to click on the preferred image to look at the photo in its original sizing or in full. A person can also see the wert einer reihe berechnen.html image gallery that we all get prepared to locate the image you are interested in.

 Hopefully you discover the image you happen to be looking for and all of us hope you want the wert einer reihe berechnen.html images which can be here, therefore that maybe they may be a great inspiration or ideas throughout the future.
Hopefully you discover the image you happen to be looking for and all of us hope you want the wert einer reihe berechnen.html images which can be here, therefore that maybe they may be a great inspiration or ideas throughout the future.
 All wert einer reihe berechnen.html images that we provide in this article are usually sourced from the net, so if you get images with copyright concerns, please send your record on the contact webpage. Likewise with problematic or perhaps damaged image links or perhaps images that don't seem, then you could report this also. We certainly have provided a type for you to fill in.
All wert einer reihe berechnen.html images that we provide in this article are usually sourced from the net, so if you get images with copyright concerns, please send your record on the contact webpage. Likewise with problematic or perhaps damaged image links or perhaps images that don't seem, then you could report this also. We certainly have provided a type for you to fill in.
 The pictures related to be able to wert einer reihe berechnen.html in the following paragraphs, hopefully they will can be useful and will increase your knowledge. Appreciate you for making the effort to be able to visit our website and even read our articles. Cya ~.
The pictures related to be able to wert einer reihe berechnen.html in the following paragraphs, hopefully they will can be useful and will increase your knowledge. Appreciate you for making the effort to be able to visit our website and even read our articles. Cya ~.

 Reihenwert berechnen - YouTube
Reihenwert berechnen - YouTube
 Reihe geometrisch unendlich alternierend Wert berechnen Konvergenz
Reihe geometrisch unendlich alternierend Wert berechnen Konvergenz






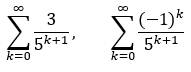 Wert der Reihe berechnen? (Mathematik, Mathematikstudium, folgen-und
Wert der Reihe berechnen? (Mathematik, Mathematikstudium, folgen-und
 Geometrische Reihe: Reihenwert bestimmen - YouTube
Geometrische Reihe: Reihenwert bestimmen - YouTube

 Grenzwert einer geometrischen Reihe bei gegebener Summenformel - YouTube
Grenzwert einer geometrischen Reihe bei gegebener Summenformel - YouTube
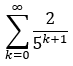 Wert der Reihe berechnen? (Mathematik, Mathematikstudium, folgen-und
Wert der Reihe berechnen? (Mathematik, Mathematikstudium, folgen-und