Observe that f ( x) does not have any relative extrema despite the fact that f ′ ( 0) = 0.

Relative extrema on a graph. To do this, find your first derivative and then find where it is equal to. In higher dimensions, saddle points are another example of critical. The x guy is where the max occurs.

An extremum is a point where a function has. (relative extrema (maxes and mins) are sometimes called local extrema.) other than just pointing these things out on the graph, we have a very specific way. Relative extrema on graph a function can have more than one relative extrema but there can only be one absolute maximum and absolute minimum point.

And this one over here is a relative minimum point. Finding all critical points and all points where is. The max is, actually, the height.

Now let's do an example dealing with absolute extrema. Notice that f ′ ( x) does not change. Local extrema (relative extrema) local extrema are the smallest or largest outputs of a small part of the function.

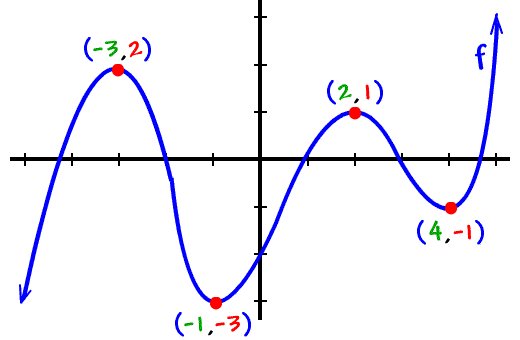
For example plot f ( x) = x 3 and note that f ′ is zero at x = 0, yet it is neither a relative maximum nor a relative minimum. F has a relative max of 1 at x = 2. Officially, for this graph, we'd say:

So we start with differentiating : So here we're told to mark the absolute maximum and the absolute. These are points that represent extreme values in some small ’neighborhood’ of the function.