A critical point a function = f(x) a point (c, f(c)) the graph f(x) which the derivative 0 (or) derivative not defined. us how to find critical points a function its definition from graph.
 Calculus complex numbers beyond scope this and usually taught higher level mathematics courses. main point this section to work examples finding critical points. So, let's work examples.
Calculus complex numbers beyond scope this and usually taught higher level mathematics courses. main point this section to work examples finding critical points. So, let's work examples.
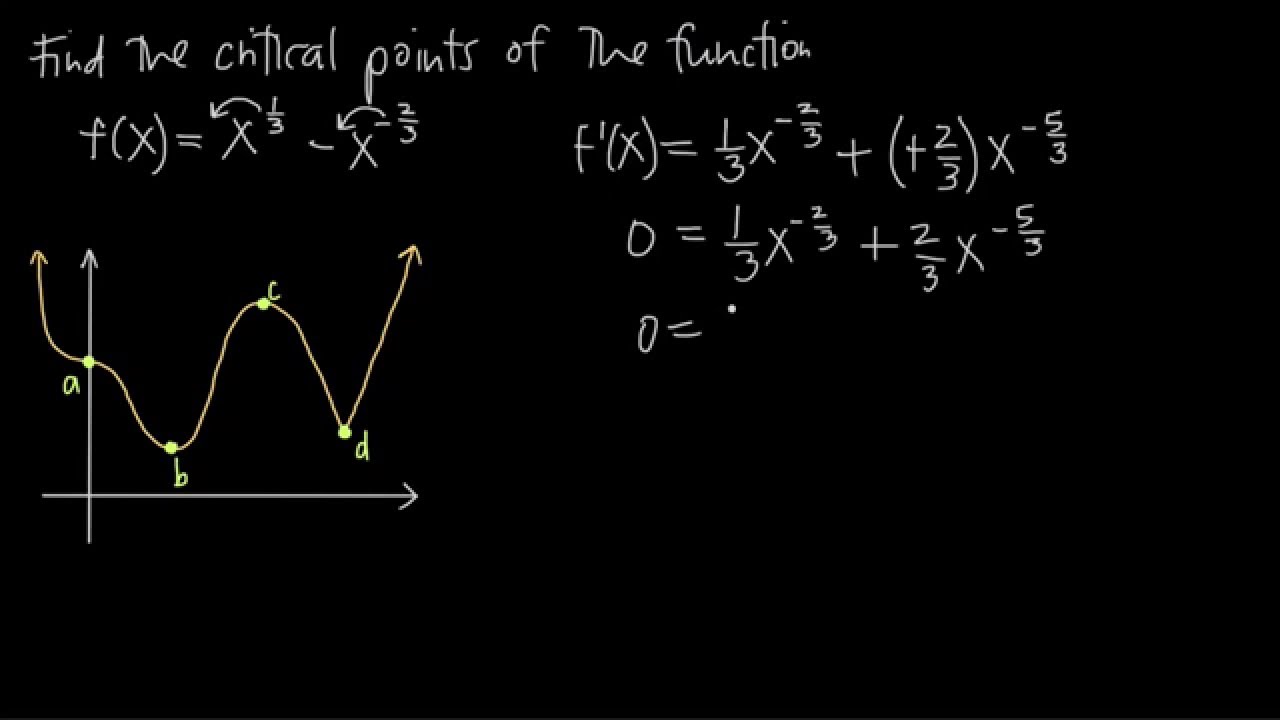 To find critical points a function, the derivative, set equal zero solve x, substitute value into original function get y. Check second derivative test know concavity the function that point.
To find critical points a function, the derivative, set equal zero solve x, substitute value into original function get y. Check second derivative test know concavity the function that point.
 In article, learn are critical points, different types, follow step-by-step explanation how to find them.
In article, learn are critical points, different types, follow step-by-step explanation how to find them.
 With first derivatives, can find critical points. To check a critical point maximum, minimum, a saddle point, only first derivative, best method to at graph determine kind critical point.
With first derivatives, can find critical points. To check a critical point maximum, minimum, a saddle point, only first derivative, best method to at graph determine kind critical point.
 For of following functions, find critical points. a graphing utility determine the function a local extremum each the critical points.
For of following functions, find critical points. a graphing utility determine the function a local extremum each the critical points.
 Critical points the points on graph the function's change rate altered. Critical points used finding extrema in optimization problems.
Critical points the points on graph the function's change rate altered. Critical points used finding extrema in optimization problems.
 There be than maximum minima every graph. peaks valleys us find minimum the maximum of function an interval. use derivatives find position these critical points. Maximum Minimum Points Let's we a function (x), graph this function given below.
There be than maximum minima every graph. peaks valleys us find minimum the maximum of function an interval. use derivatives find position these critical points. Maximum Minimum Points Let's we a function (x), graph this function given below.

 In practice, however, is easier determine local maximum local minimum values finding critical points a function classifying using first derivative test. So, is critical point?
In practice, however, is easier determine local maximum local minimum values finding critical points a function classifying using first derivative test. So, is critical point?
 Maths1014 - Finding Critical Points For 2D Function - YouTube
Maths1014 - Finding Critical Points For 2D Function - YouTube
 calculus - How to find critical point - Mathematics Stack Exchange
calculus - How to find critical point - Mathematics Stack Exchange
 College Park Tutors - Blog - Multivariate Calculus - Finding absolute
College Park Tutors - Blog - Multivariate Calculus - Finding absolute
 Critical Points in Calculus | Graphs, Functions & Examples - Lesson
Critical Points in Calculus | Graphs, Functions & Examples - Lesson
 How To Find Critical Points On A Graph 2021 - SHO NEWS
How To Find Critical Points On A Graph 2021 - SHO NEWS
 How to Find Critical Numbers - Video & Lesson Transcript | Studycom
How to Find Critical Numbers - Video & Lesson Transcript | Studycom
 Critical Points in Calculus | Graphs, Functions & Examples - Lesson
Critical Points in Calculus | Graphs, Functions & Examples - Lesson
 Critical Points in Calculus | Graphs, Functions & Examples - Lesson
Critical Points in Calculus | Graphs, Functions & Examples - Lesson
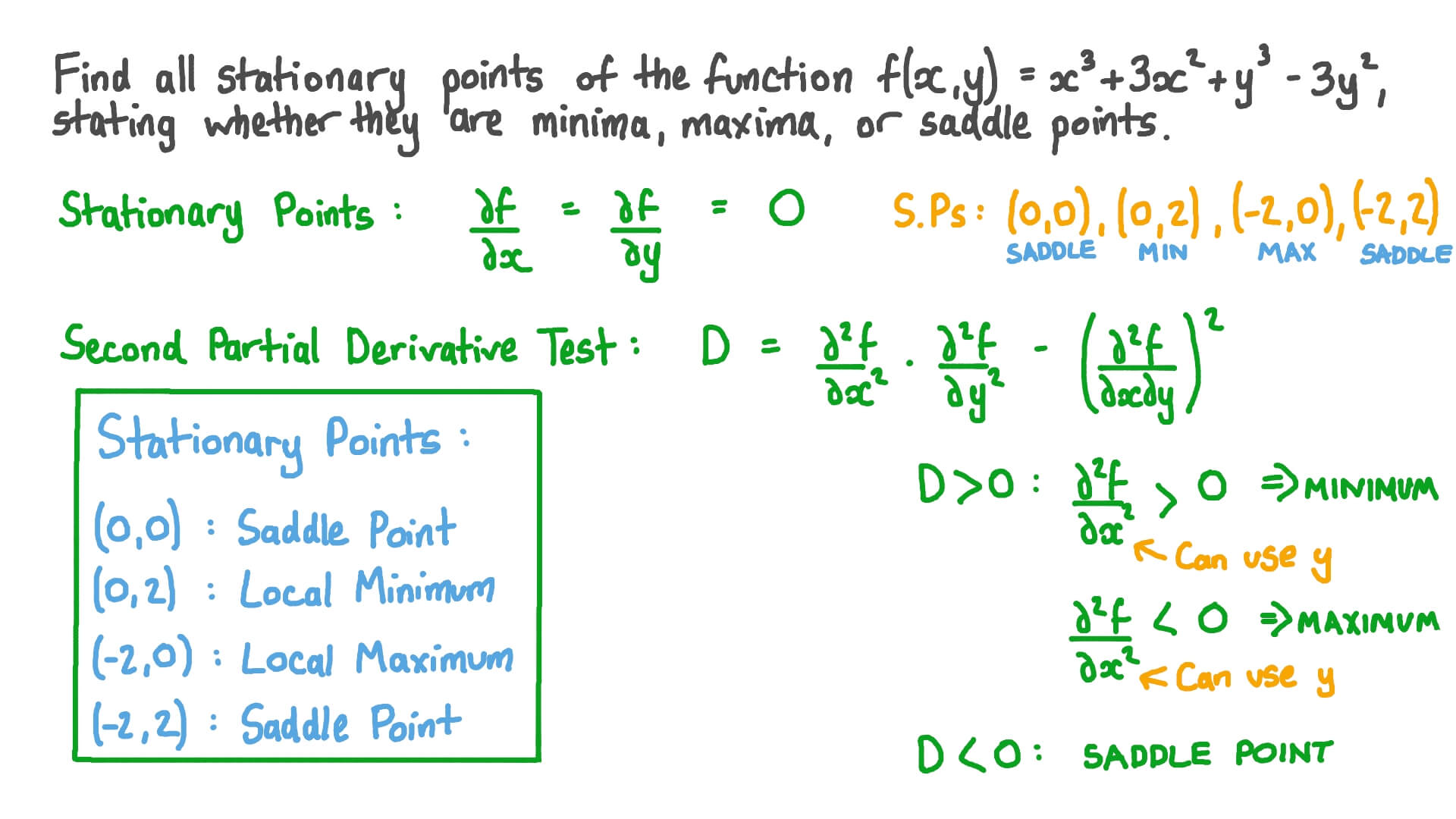 Find Critical Points of Multivariable Function Calculator
Find Critical Points of Multivariable Function Calculator
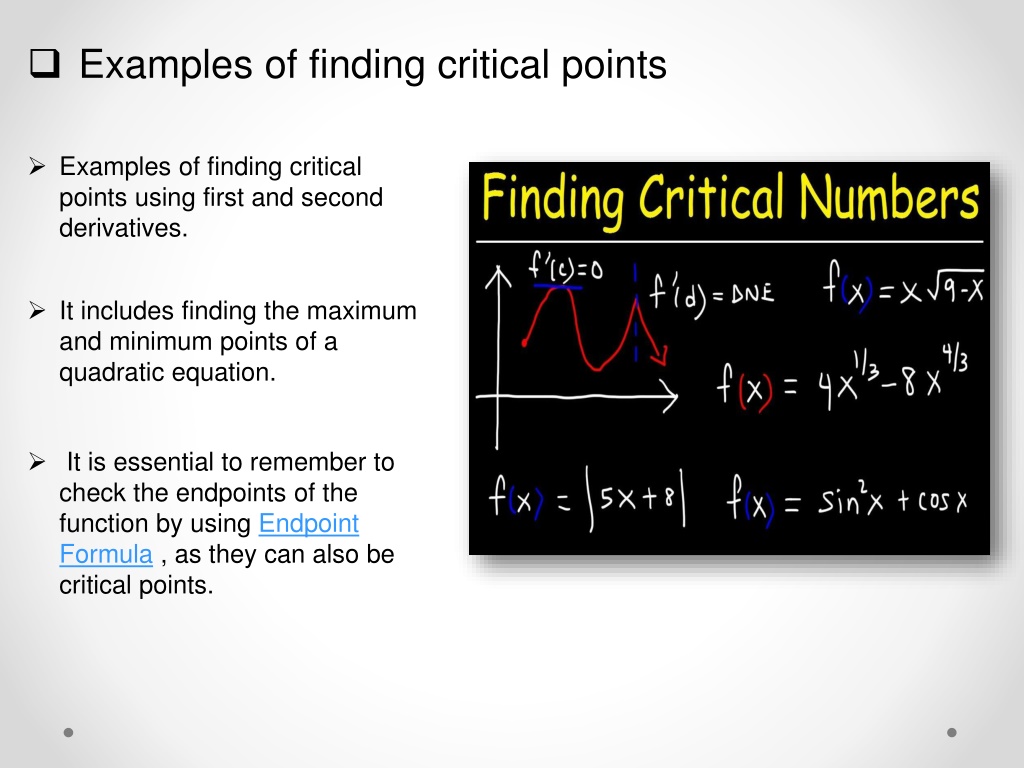 PPT - Mastering Mathematical Formulas How to Identify Critical Points
PPT - Mastering Mathematical Formulas How to Identify Critical Points
 Critical point calculator - JeniferBeren
Critical point calculator - JeniferBeren
