Which of the following is true about the graph of.

Graphing a logarithmic function basic. Practice graphing a basic logarithmic function with practice problems and explanations. Boost your algebra grade with. Consider the graph of the function y = log 2 ( x).

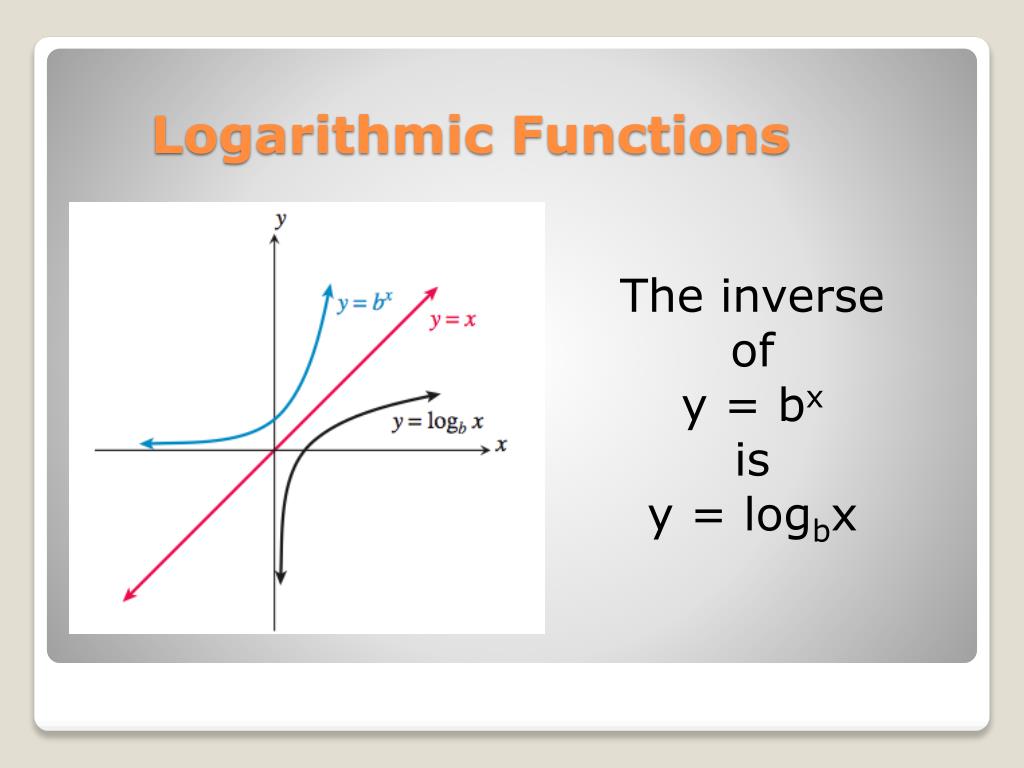
We first start with the properties of the graph of the basic logarithmic function of base a, f (x) = log a (x) , a > 0 and a not equal to 1. Exponential and logarithmic functions are inverses of each other. To graph logarithmic functions we can plot points or identify the basic function and use the transformations.

We have already seen that the domain of the basic logarithmic function y = log a x is the set of positive real numbers and the range is the set of all real numbers. Review properties of logarithmic functions. The domain is infinite in both directions.

It is an odd function. This video provides detailed instructions for graphing a logarithmic function. Since b = 5 is greater than one, we know the function is increasing.the left tail of the graph will approach.

Now that we have a feel for the set of values for which a logarithmic function is defined, we move on to graphing logarithmic functions. Before graphing, identify the behavior and key points for the graph. The logarithmic function, or the log function for short, is written as f(x) = log baseb (x), where b is the base of the logarithm and x is greater than 0.

Graphs of basic logarithmic functions. Logarithms are simply another way to write exponents. Be sure to indicate that there is a vertical asymptote by using a.