Represent this scenario in a graph.

Finding increasing and decreasing intervals. Let's try to identify where the function is increasing, decreasing, or constant in one sweep. Then set f' (x) = 0. When f’(c) = 0 or is undefined → c is a critical number.

Want to save money on printing? Laura has observed that the level of water in her sink is decreasing as it drains. Let's evaluate at each interval to see if it's positive or negative on that interval.

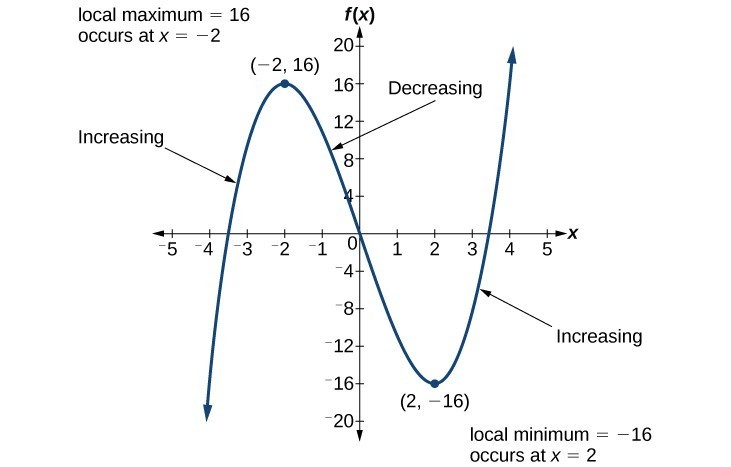
We can find the increasing and decreasing regions of a function from its graph, so one way of answering this question is to sketch the curve, ℎ ( 𝑥) = − 1 7 − 𝑥 − 5. For the following exercises, use the graph of each function to estimate the intervals on which the function is increasing or decreasing.here are all of our m. Take a pencil or a pen.

Increasing/decreasing intervals increasing when \(f'(x)\gt 0\) decreasing when \(f'(x)\lt 0\) practice problems for each function a. The given function is f ( x) = x 200 − x 100, and i'm supposed to find it's decreasing and increasing intervals. Identify the input variable, the output variable and the intervals.

(i) it is not increasing. (ii) decreasing for 0 < x < 2. Find the leftmost point on the graph.

Absolute value, algebra 2 and. To find whether a function is decreasing or increasing along an interval, we look at the critical values and use what we call the first derivative test. Also, i should find them not by using derivatives but by doing function.