
As a result we reject the null hypothesis.
Example of hypothesis for multiple regression. All the coefficients equal to zero. Y taste x1 acetic acid x2 hydrogen sulfide x3 lactic acid Our hypothesis is as follows. Regression model we will always take a composite hypothesis as an alternative hypothesis.
This hypothesis which shall be called H 1 is formulated using the operator. The general regression for the. Partition the vector of regression coefficients as β β1 β2 where β1 is p1r1 and β2 is r 1.
0000 we can reject H 0 and be confident that not all the slopes are equal to 0. Third multiple regression offers our first glimpse into statistical models that use more than two quantitative variables. Range we will reject the null hypothesis.
Welcome to Minitab press F1 for help. Multiple Linear Regression Y1 vs X1 X2. There will be no significant prediction of insert dependent variable by insert predictor variable 1 and insert predictor variable 2 etc.
At least one βj is not 0 Given our small p-value Sig. For our example α 05 which is equal to the upper limit of the p-value. Note when defining Alternative Hypothesis I have used the words at least one.
As you are doing a multiple regression there is also a null hypothesis. Here are two templates for a Multiple Linear Regression Null-Hypotheses. For this example given the sample size etc lets say the R²-change will be significant if the average contribution of the added predictors is 5 05 Lets also say that two of the four predictors x1 x2 have contributions of 8 each and two x3 and x4 have contributions of 4 each.






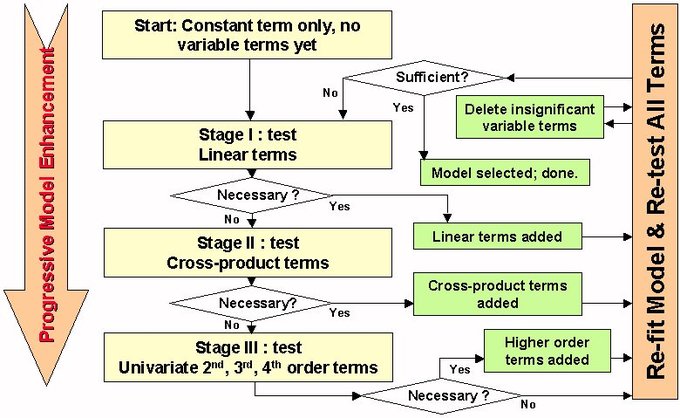









/dotdash_Final_Multiple_Linear_Regression_MLR_Sep_2020-01-b2cd0ecf1b69417e890d8ab0a7cff366.jpg)


