Hello, in this particular article you will provide several interesting pictures of example of conjunction elimination.html. We found many exciting and extraordinary example of conjunction elimination.html pictures that can be tips, input and information intended for you. In addition to be able to the example of conjunction elimination.html main picture, we also collect some other related images. Find typically the latest and best example of conjunction elimination.html images here that many of us get selected from plenty of other images.
 We all hope you can get actually looking for concerning example of conjunction elimination.html here. There is usually a large selection involving interesting image ideas that will can provide information in order to you. You can get the pictures here regarding free and save these people to be used because reference material or employed as collection images with regard to personal use. Our imaginative team provides large dimensions images with high image resolution or HD.
We all hope you can get actually looking for concerning example of conjunction elimination.html here. There is usually a large selection involving interesting image ideas that will can provide information in order to you. You can get the pictures here regarding free and save these people to be used because reference material or employed as collection images with regard to personal use. Our imaginative team provides large dimensions images with high image resolution or HD.
 example of conjunction elimination.html - To discover the image more plainly in this article, you are able to click on the preferred image to look at the photo in its original sizing or in full. A person can also see the example of conjunction elimination.html image gallery that we all get prepared to locate the image you are interested in.
example of conjunction elimination.html - To discover the image more plainly in this article, you are able to click on the preferred image to look at the photo in its original sizing or in full. A person can also see the example of conjunction elimination.html image gallery that we all get prepared to locate the image you are interested in.
 We all provide many pictures associated with example of conjunction elimination.html because our site is targeted on articles or articles relevant to example of conjunction elimination.html. Please check out our latest article upon the side if a person don't get the example of conjunction elimination.html picture you are looking regarding. There are various keywords related in order to and relevant to example of conjunction elimination.html below that you can surf our main page or even homepage.
We all provide many pictures associated with example of conjunction elimination.html because our site is targeted on articles or articles relevant to example of conjunction elimination.html. Please check out our latest article upon the side if a person don't get the example of conjunction elimination.html picture you are looking regarding. There are various keywords related in order to and relevant to example of conjunction elimination.html below that you can surf our main page or even homepage.
 Hopefully you discover the image you happen to be looking for and all of us hope you want the example of conjunction elimination.html images which can be here, therefore that maybe they may be a great inspiration or ideas throughout the future.
Hopefully you discover the image you happen to be looking for and all of us hope you want the example of conjunction elimination.html images which can be here, therefore that maybe they may be a great inspiration or ideas throughout the future.
 All example of conjunction elimination.html images that we provide in this article are usually sourced from the net, so if you get images with copyright concerns, please send your record on the contact webpage. Likewise with problematic or perhaps damaged image links or perhaps images that don't seem, then you could report this also. We certainly have provided a type for you to fill in.
All example of conjunction elimination.html images that we provide in this article are usually sourced from the net, so if you get images with copyright concerns, please send your record on the contact webpage. Likewise with problematic or perhaps damaged image links or perhaps images that don't seem, then you could report this also. We certainly have provided a type for you to fill in.
 The pictures related to be able to example of conjunction elimination.html in the following paragraphs, hopefully they will can be useful and will increase your knowledge. Appreciate you for making the effort to be able to visit our website and even read our articles. Cya ~.
The pictures related to be able to example of conjunction elimination.html in the following paragraphs, hopefully they will can be useful and will increase your knowledge. Appreciate you for making the effort to be able to visit our website and even read our articles. Cya ~.
 PPT - Logic PowerPoint Presentation, free download - ID:3028504
PPT - Logic PowerPoint Presentation, free download - ID:3028504
 PPT - Methods of Proof involving PowerPoint Presentation, free download
PPT - Methods of Proof involving PowerPoint Presentation, free download
 Subordinate Conjunction Vs Coordinating Conjunction
Subordinate Conjunction Vs Coordinating Conjunction
 An Easy Guide to Conjunctions (with Conjunction Examples) • 7ESL
An Easy Guide to Conjunctions (with Conjunction Examples) • 7ESL
 10 examples of conjunction in a sentence - Artofit
10 examples of conjunction in a sentence - Artofit
 List Of Conjunctions For Kids
List Of Conjunctions For Kids
 Conjunction and Its Types with Examples (List of Conjunctions
Conjunction and Its Types with Examples (List of Conjunctions
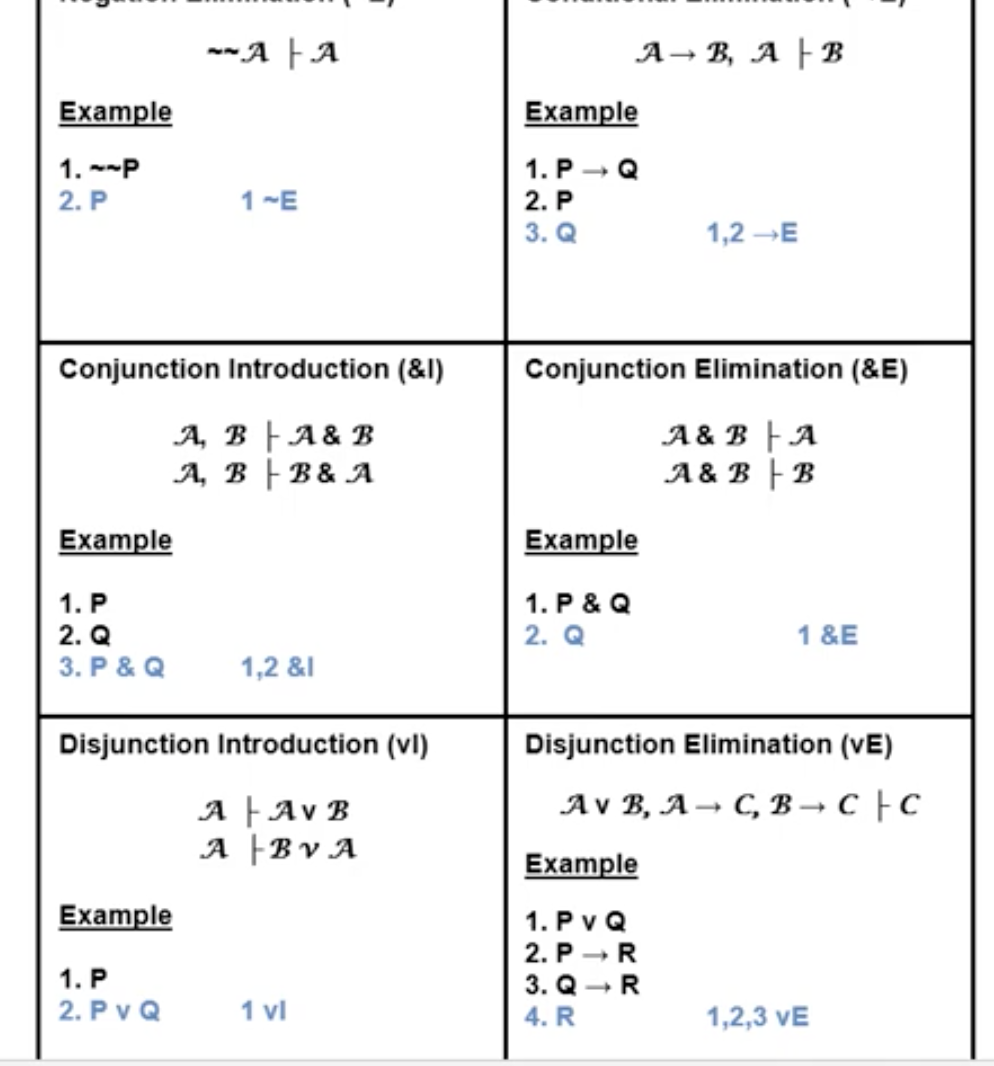 Solved 4 Derive the following in propositional logic using | Cheggcom
Solved 4 Derive the following in propositional logic using | Cheggcom
 20 Examples of Conjunction are in Sentences
20 Examples of Conjunction are in Sentences
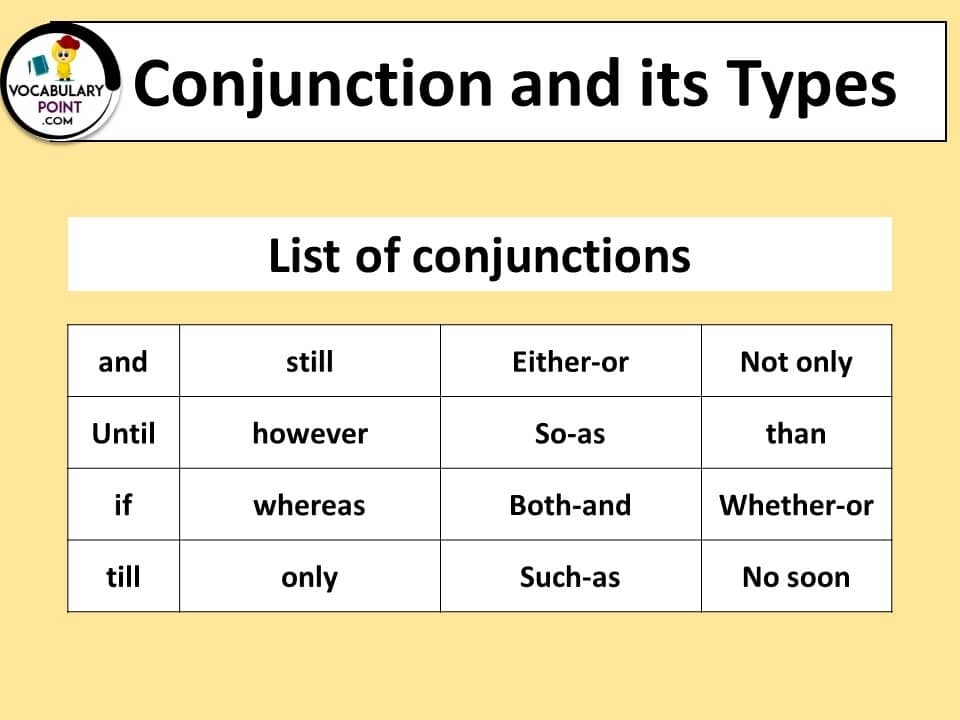 Conjunction and Its Types with Examples (List of Conjunctions
Conjunction and Its Types with Examples (List of Conjunctions
 20 Examples of Conjunction are in Sentences
20 Examples of Conjunction are in Sentences
 100 Examples of Conjunctions in Sentences
100 Examples of Conjunctions in Sentences
 Conjunction Examples Grade 4
Conjunction Examples Grade 4
 10 Examples of Conjunctions in Sentences - EngDic
10 Examples of Conjunctions in Sentences - EngDic